Counting by numbers

Can bees count?

If they can count, what’s the highest number they can count to?

Do they understand the concept of ‘more than’ or ‘less than’? And what about zero? These are very much more complex concepts than simple numbers.

If bees have simple counting skills, can they do mathematics? Addition, subtraction, multiplication and division?

What about more complicated maths like differential equations or Fourier transforms? {{1}}

And finally, if we can determine the answer to all these questions, do we know how bees count? Do they simply see things and think “Ah Ha! Two flowers each with four petals”, or do they count in a non-numerical way?

Numbers, arithmetic, more than, less than, zero etc. are complicated concepts that involve aspects of neuroscience, psychology and even philosophy. I’m a molecular biologist/virologist and so singularly ill-equipped to understand the more esoteric or advanced aspects of these topics.

Don’t say I didn’t warn you 😉

Can bees count?

Yes.

Bees, like many other animals have basic counting skills.

In studies going back 25 years, Lars Chittka {{2}} demonstrated that bees exhibited what he called protocounting. He positioned a feeder between distinctive landmarks (tents in a field) and showed – by altering the number of tents between the hive and the feeder – that the ability of the bees to find the feeder was at least partly due to their ability to count the landmarks.

Counting by bees

If he added more tents between the feeder {{3}} and the hive, the bees flew a shorter distance to where they thought the food supply was. If he removed some of the landmarks, the bees flew further.

Chittka used the term protocounting because he reasoned that the things that the bees were counting – in this case tents in a row in a field – may not be transferrable to different objects. For example, bees trained to a feeder between tents 3 and 4 in a series might not return to the same position in a series of trees in a row. He didn’t test this, but others now have.

Bees also measure distance flown and this had a greater influence on where the bees searched in the series of landmarks. Nevertheless, these early studies provided compelling evidence that bees had some basic counting skills … or numerosity as it is called.

Is this ‘just’ protocounting and how high can they count?

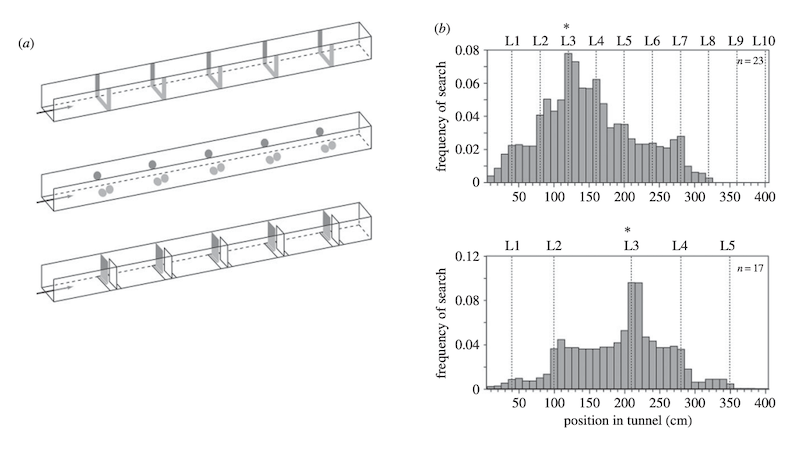
To understand numerosity in more detail scientists moved the experiments into a laboratory setting where they could control the environment much more tightly.

Landmark counting in a laboratory flight tunnel

These use uniform flight tunnels containing painted or taped on landmarks. For some of the detail read the legend in the figure above {{4}}. By using flight tunnels they could change the landmarks – see (a) above – from stripes to dots to baffles. In doing so they demonstrated that the bees were counting landmarks per se, rather than a particular type of landmark.

For example, bees trained to search for food between the third and fourth set of stripes would look between the third and fourth set of dots. This is much more advanced than the protocounting proposed in the initial study by Chittka and colleagues. … it shows a degree of abstract numerosity.

The use of baffles prevented the bees ‘looking ahead’ (or behind) to visualise the entire set of landmarks together … they had to keep a running total in their heads.

Finally, the highly controlled environment of a flight tunnel enabled the researchers to determine that bees could count up to … wait for it … four.

Not a huge number but, in terms of cognition, a significant advance on none, one or more.

But let’s not get ahead of ourselves.

We’re going to tackle the concept of zero and ‘more than’ in a minute.

It has been argued that the upper limit of four – a limit shared with a number of other animals – might be a consequence of the small size of the bee’s brain {{5}} and the small percentage of the neurones in the brain being dedicated to counting {{6}}.

However, it may represent a more fundamental limit of cognition and perception that reflects the capacity limit of working memory. This isn’t restricted to bees … it’s something shared with beekeepers. For more detail on this I recommend Nelson Cowan’s The magical number 4 in short-term memory: A reconsideration of mental storage capacity. {{7}}

Go on … knock yourself out 😉

More or less … and zero is not a number

Actually, it is.

What’s more, it’s an even number … 0, 2, 4, 6, 8 are the first five even numbers from zero.

It’s the ’empty set’, smaller than one.

It’s also, conceptually, a difficult number to grasp. Children take much longer to understand that zero is a number (e.g. that they can do maths with) than they do to understand that zero means “nothing”.

There are four steps defined in the “acquisition of the understanding of zero in human history, psychology, animal cognition and neurophysiology” {{8}}, which are:

1. defining zero as ‘nothing’
2. the categorical definition of zero as ‘nothing’ versus ‘something’
3. an appreciation that zero is a quantity at the low end of the positive integer numerical continuum (see above)
4. the symbolic representation of zero i.e. 0, the Arabic number for use in maths

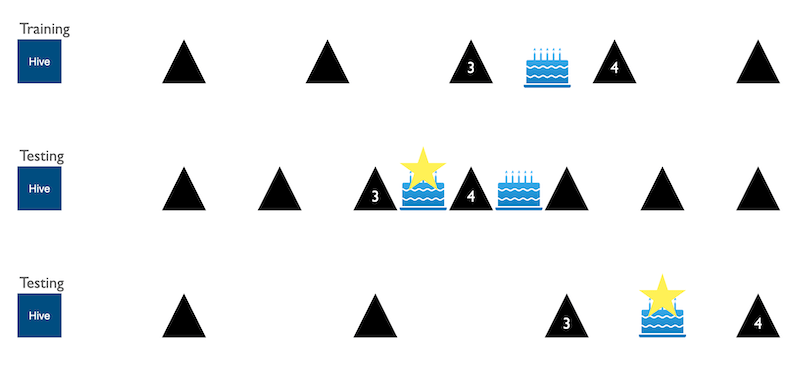
Can bees distinguish ‘more than’ or ‘less than’? And what about zero being ‘less than’ one?

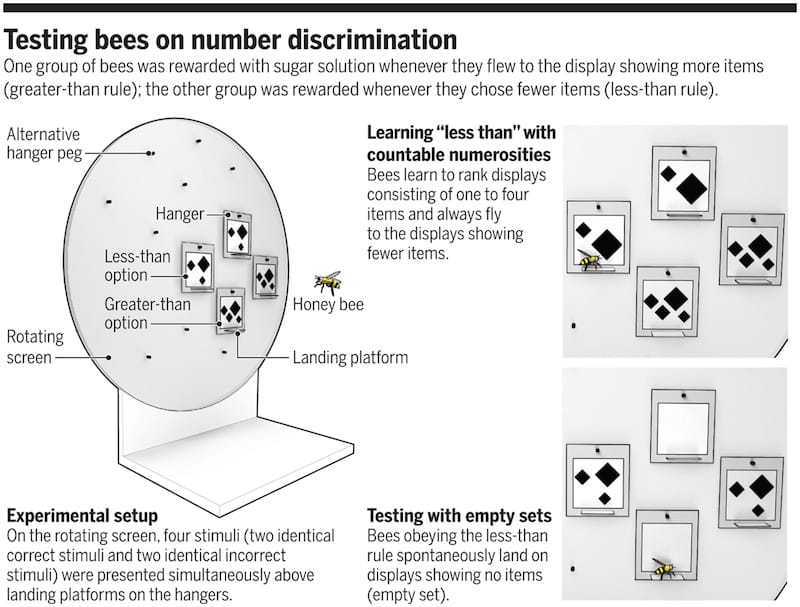
The experiments to determine this were simple but elegant (as all the best experiments are {{9}}) and involved training and rewarding bees to select targets that displayed more items or fewer items.

Bees trained to select ‘more than’ targets would choose one displaying four items over one with two or three. Similarly, the ‘less than’ trainees {{10}} would select two items rather than three or four.

More than, less than and zero

These experiments confirmed that bees ‘understood’ the concepts of more than or less than. The experiments were controlled to exclude the possibility that the bees were responding to other stimuli that changed in the target e.g. signal density or colour intensity.

And if that wasn’t enough {{11}} they also showed that the ‘less than’ trainees would choose an empty target when offered the choice between ‘some’ and ‘none’.

But there’s more … or less

The ‘popularity’ of the empty set – zero items – was directly related to the difference in the number of items displayed on the non-empty targets. For example, bees more frequently chose the zero option when numbers were numerically more distant (0 vs. 5 or 0 vs. 6) than those closer together (0 vs. 1 or 0 vs. 2).

This relationship between accuracy and numerical distance is called Weber’s law.

This demonstrates a significant degree of understanding of the place of zero in a numerical continuum, an extraordinary feat in a honey bee.

This appreciation of the concept of zero as a number is similar in ability to that shown by African grey parrots, non-human primates … and pre-school children.

That’s impressive.

Counting by numbers

These numerical skills, amazing as they are {{12}} demonstrate an appreciation of numbers, but not the ability to manipulate numbers.

Can bees count?

For example, could bees solve this testing little equation?

Maxwell’s equation – the foundation of classical magnetism, optics and electric circuits … but you knew that already

OK, not so fast … is that really a fair test?

These coupled partial differential equations are quite challenging. As bees have yet to be trained to hold a piece of chalk, they can’t write QED {{13}} at the bottom of the blackboard to indicate they’ve solved it.

So what about these instead?

1 + 1 = 2

3 – 1 = 2

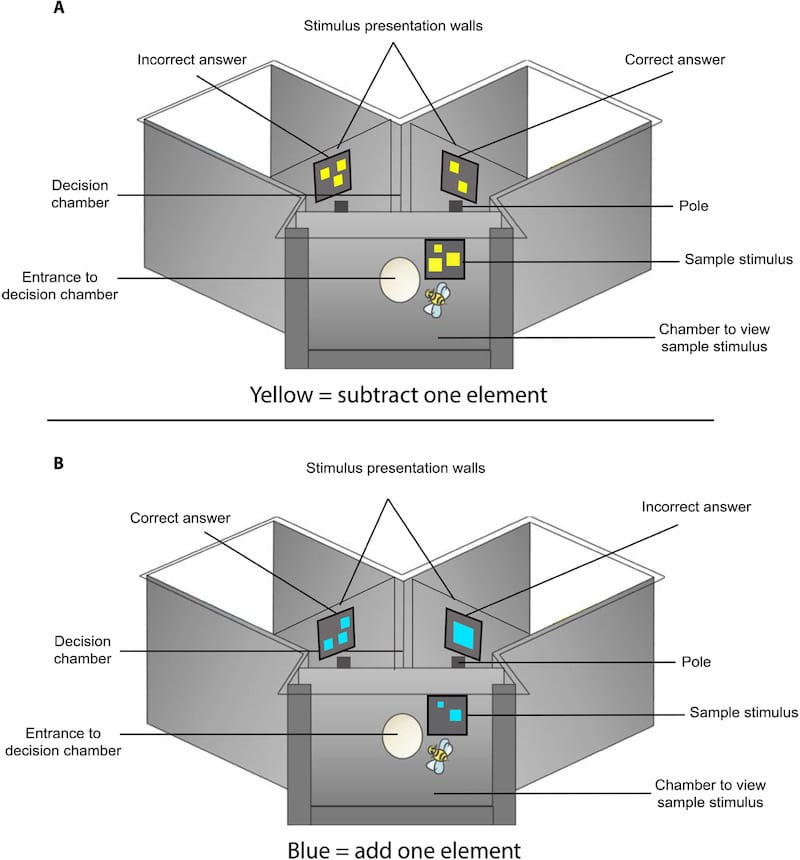
To test this Adrian Dyer {{14}} and colleagues substituted colours for mathematical operands during the training e.g. blue for addition, yellow for subtraction, coupled with shapes for the numbers.

Y shaped maze to determine if bees can do maths

They trained the bees using a classical reward-punishment system. This sounds worse than it is. It means they received delicious syrup {{15}} when they got the right answer, but bitter-tasting quinine when they got the wrong answer.

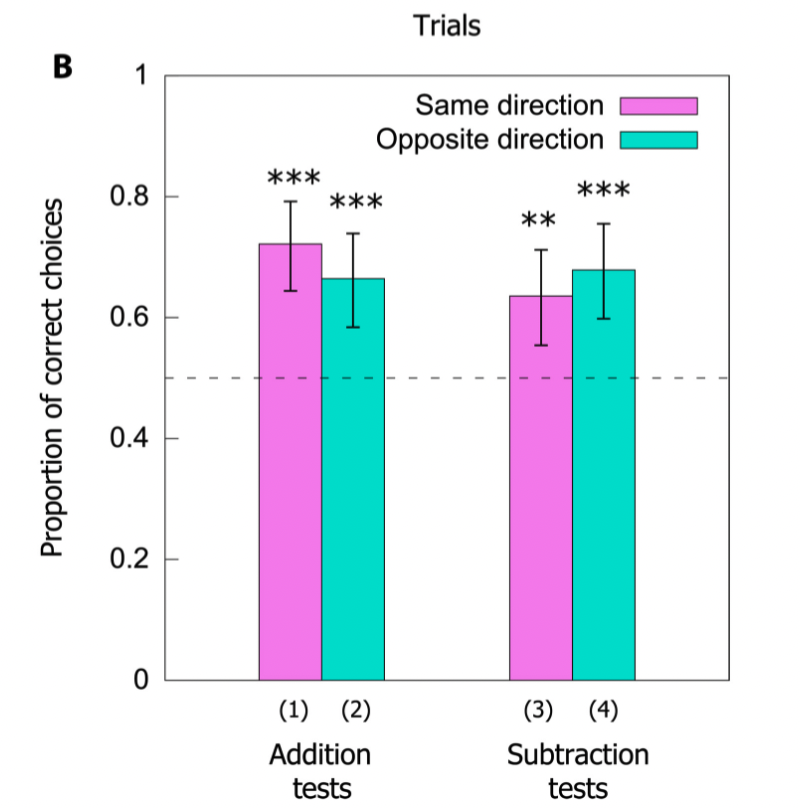
The more training the bees received, the better they got at maths – both addition and subtraction. Once trained, the bees were tested.

Honey bees can do basic maths

In this subsequent testing phase the bees got the correct answer about 75% of the time. If they had been choosing the answer at random they would have achieved only ~50% of correct answers.

So, if more than, less than and an appreciation of zero aren’t enough, bees can also do mathematics.

Though probably not partial differential equations 😉

How do bees count?

It’s not yet clear how bees actually count objects – like the shapes scientists train them to recognise in the Y shaped maze shown further up this post.

Numerical cognition is considered a higher cognitive activity. In humans we’ve abstracted the process and – for at least the last 1100 years – used Arabic numbers to indicate quantities of ‘stuff’.

Of course, humans could count long before this, as could the apes from which we are descended. But they don’t use Arabic numerals and nor do bees.

3 + 1 = 4

Humans can look at a diagram like the one above and immediately recognise and count the similar shapes – this is a process called subitizing and is restricted to small numbers of shapes. You can train computers to do the same thing using neural networks, object detection and counting the instances of the objects detected.

However this is both computationally expensive and exploits symbolic mathematics, neither of which are achievable in the tiny brain of a honey bee. They cannot inspect a complete field of view and conclude “four apples”, or “three black circles”.

Bees cannot subitize … their brains don’t work fast enough and their visual acuity, and compound eyes, are probably incompatible with the process.

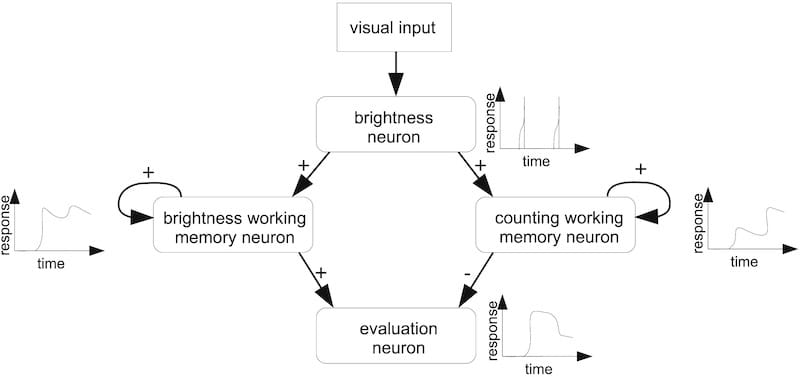
Instead, recent modelling studies have suggested that bees might count objects by serial sequential processing.

If you observe honey bees traversing a Y shaped maze they closely inspect each and every element in the patterns they are presented with.

Simple neural model for counting in honey bees

Using just four neurones, this method appears to allow the bee to achieve the known capabilities of their numerosity i.e. counting to four, concepts of more than or less than, understanding zero, and the fulfilment of Weber’s Law.

This area of the science is even more outside my comfort zone than Maxwell’s equation (see above) and I recommend you read the article cited in the legend to the figure above for further details.

Unanswered questions

There’s clearly a lot more to understand about the numerical and mathematical abilities of honey bees. This will take time, but good progress has been made over the last decade or so.

A full understanding of the neuronal processing involved in object discrimination and counting will probably require an ability to determine which neurones are firing, and the pathways of neuronal communication.

Scientists are years away from being able to do this with honey bees. It necessitates the ability to introduce specific reporter genes (for example that turn green when a neurone fires) into individual cell lineages. We don’t have the tools to do this (yet), but it can be done with fruit flies (Drosophila) and some of the same methods do – or might – work in bees.

In the meantime it’s worth thinking about what the ability to count contributes to the biology and behaviour of bees.

Do plants with more petals have more nectaries, and do bees follow these numerical clues rather than – or in addition to – other visual or scent stimuli?

And why on earth do bees have the ability to do basic maths?

I can’t think of an advantage that this would confer to bees.

Can you?

Notes

The title of this post was going to be ‘0 … 1 … 2 … 3 … 4 … more’ but that would have looked terrible as a URL and would have sunk without trace in Google searches.

Instead I’ve used a play on the title of the 1988 Peter Greenaway film Drowning by Numbers. This has a fairy tale-like plot that involves three generations of women – all called Cissie Colpitts – drowning their husbands. Bernard Hill plays Madgett, the coroner encouraged to cover up the crimes and involves a series of invented games, one of which is called ‘Bees in the Trees’ (which seemed appropriate).

Drowning by Numbers … going by the number in the background, a scene from about half way through the film

If you’ve not seen the film (and enjoy slightly surreal movies and black comedies) I can recommend it. See if you can count the numbers 1 to 100 that appear, almost all in sequence, either in the background or spoken by the characters. Michael Nyman wrote the music which is similarly highly structured, and based entirely upon a Mozart Sinfonia Concertante in E flat.

Of course Counting by numbers is also relevant as bees probably count in a different way altogether. Perhaps I should have ended the title of the post with a question mark?

{{1}}: I’ll not be covering either of these last two as I can’t do them myself. If bees could it would make me look and feel even more stupid, so I’ll avoid the subject altogether.

{{2}}: Chittka, L., and Geiger, K. (1995). Can honey bees count landmarks? Anim. Behav. 49, 159–164.

{{3}}: I’ve used a cake to indicate the feeder … it was syrup in the actual experiment.

{{4}}: You need to click on the figure to see a larger version and reveal the legend.

{{5}}: ~1% that of a human child … measured in neurones, not volume.

{{6}}: Further studies have suggested that bees may be able to count numbers larger than four if trained in the right way … I’ll return to this in a future post as I understand even less of the science than I do of the stuff presented here …

{{7}}: Cowan, N. (2001). The magical number 4 in short-term memory: A reconsideration of mental storage capacity. Behavioral and Brain Sciences, 24, 87-114.

{{8}}: Howard et al., (2018) Numerical ordering of zero in honey bees. Science 360:1124-1126.

{{9}}: And some of mine singularly are not.

{{10}}: This ‘rewarding’ always involves sugar syrup (not cake) … bees are easy to please.

{{11}}: And the reason this paper was published in one of the top scientific journals.

{{12}}: And if you don’t think they’re amazing then you have no soul then you should … the brain of a bee has about 85 million neurones fewer than the brain of a child.

{{13}}: Quod erat demonstrandum

{{14}}: Who was also the senior author on the paper that showed the understanding of zero by bees.

{{15}}: Not cake.